Pythagorean tuning

Pythagorean tuning (Greek: Πυθαγόρεια κλίμακα) is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2 (the perfect fifth), "found in the harmonic series."[1] This interval is chosen because it is one of the most consonant. Attributed to Pythagoras (sixth century BC), "the Pythagorean system would appear to be ideal because of the purity, of the fifths, but other intervals, particularly the major third, are so badly out of tune that major chords [may be considered] a dissonance."[1][2]

The Pythagorean scale is any scale which may be constructed from only perfect fifths and octaves[3] or the gamut of (all 12) pitches constructed from only perfect fifths and octaves and from which specific scales may be drawn. See: generated collection. For example, the series of fifths generated above gives seven notes, a diatonic major scale on C in Pythagorean tuning, shown in notation on the top right.

Contents

Method

Pythagorean tuning is based on a stack of intervals called perfect fifths, each tuned in the ratio 3:2, the next simplest ratio after 2:1. Starting from D for example (D-based tuning), six other notes are produced by moving six times a ratio 3:2 up, and the remaining ones by moving the same ratio down:

E♭—B♭—F—C—G—D—A—E—B—F♯—C♯—G♯

This succession of eleven 3:2 intervals spans across a wide range of frequency (on a piano keyboard, it encompasses 77 keys). Since notes differing in frequency by a factor of 2 are given the same name, it is customary to divide or multiply the frequencies of some of these notes by 2 or by a power of 2. The purpose of this adjustment is to move the 12 notes within a smaller range of frequency, namely within the interval between the base note D and the D above it (a note with twice its frequency). This interval is typically called the basic octave (on a piano keyboard, an octave encompasses only 13 keys ).

For instance, the A is tuned such that its frequency equals 3:2 times the frequency of D — if D is tuned to a frequency of 288 Hz, then A is tuned to 432 Hz. Similarly, the E above A is tuned such that its frequency equals 3:2 times the frequency of A, or 9:4 times the frequency of D — with A at 432 Hz, this puts E at 648 Hz. Since this E is outside the above-mentioned basic octave (i.e. its frequency is more than twice the frequency of the base note D), it is usual to halve its frequency to move it within the basic octave. Therefore, E is tuned to 324 Hz, a 9:8 above D. The B at 3:2 above that E is tuned to the ratio 27:16 and so on. Starting from the same point working the other way, G is tuned as 3:2 below D, which means that it is assigned a frequency equal to 2:3 times the frequency of D — with D at 288 Hz, this puts G at 192 Hz. This frequency is then doubled (to 384 Hz) to bring it into the basic octave.

When extending this tuning however, a problem arises: no stack of 3:2 intervals (perfect fifths) will fit exactly into any stack of 2:1 intervals (octaves). For instance a stack such as this, obtained by adding one more note to the stack shown above

A♭—E♭—B♭—F—C—G—D—A—E—B—F♯—C♯—G♯

will be similar but not identical in size to a stack of 7 octaves. More exactly, it will be about a quarter of a semitone larger (see Pythagorean comma). Thus, A♭ and G♯, when brought into the basic octave, will not coincide as expected. The table below illustrates this, showing for each note in the basic octave the conventional name of the interval from D (the base note), the formula to compute its frequency ratio, its ratio, its size in cents, and the difference (ET-dif) in cents between its size and the size of the corresponding one in the equally tempered scale.

Note Interval from D Formula Frequency
ratio		 Size
(cents)		 ET-dif
(cents)
A♭ diminished fifth 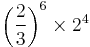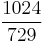\left( \frac{2}{3} \right) ^6 \times 2^4 \frac{1024}{729} 588.27 -11.73
E♭ minor second 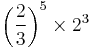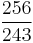\left( \frac{2}{3} \right) ^5 \times 2^3 \frac{256}{243} 90.22 −9.78
B♭ minor sixth 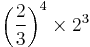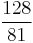\left( \frac{2}{3} \right) ^4 \times 2^3 \frac{128}{81} 792.18 −7.82
F minor third 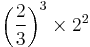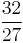\left( \frac{2}{3} \right) ^3 \times 2^2 \frac{32}{27} 294.13 −5.87
C minor seventh 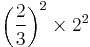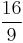\left( \frac{2}{3} \right) ^2 \times 2^2 \frac{16}{9} 996.09 −3.91
G perfect fourth 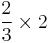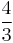\frac{2}{3} \times 2 \frac{4}{3} 498.04 -1.96
D unison 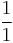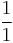\frac{1}{1} \frac{1}{1} 0 .00 0.00
A perfect fifth 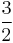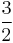\frac{3}{2} \frac{3}{2} 701.96 1.96
E major second 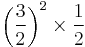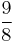\left( \frac{3}{2} \right) ^2 \times \frac{1}{2} \frac{9}{8} 203.91 3.91
B major sixth 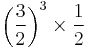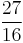\left( \frac{3}{2} \right) ^3 \times \frac{1}{2} \frac{27}{16} 905.87 5.87
F♯ major third 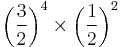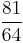\left( \frac{3}{2} \right) ^4 \times \left( \frac{1}{2} \right) ^2 \frac{81}{64} 407.82 7.82
C♯ major seventh 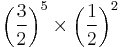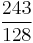\left( \frac{3}{2} \right) ^5 \times \left( \frac{1}{2} \right) ^2 \frac{243}{128} 1109.78 9.78
G♯ augmented fourth 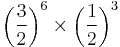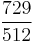\left( \frac{3}{2} \right) ^6 \times \left( \frac{1}{2} \right) ^3 \frac{729}{512} 611.73 11.73

In the formulas, the ratios 3:2 or 2:3 represent an ascending or descending perfect fifth (i.e. an increase or decrease in frequency by a perfect fifth), while 2:1 or 1:2 represent an ascending or descending octave.

The major scale based on C, obtained from this tuning is[4]:

Note C D E F G A B C
Ratio 1/1 9/8 81/64 4/3 3/2 27/16 243/128 2/1
Step — 9/8 9/8 256/243 9/8 9/8 9/8 256/243 —

In equal temperament, pairs of enharmonic notes such as A♭ and G♯ are thought of as being exactly the same note — however, as the above table indicates, in Pythagorean tuning they have different ratios with respect to D, which means they are at a different frequency. This discrepancy, of about 23.46 cents, or nearly one quarter of a semitone, is known as a Pythagorean comma.

To get around this problem, Pythagorean tuning ignores A♭, and uses only the 12 notes from E♭ to G♯. This, as shown above, implies that only eleven just fifths are used to build the entire chromatic scale. The remaining fifth (from G♯ to E♭) is left badly out-of-tune, meaning that any music which combines those two notes is unplayable in this tuning. A very out-of-tune interval such as this one is known as a wolf interval. In the case of Pythagorean tuning, all the fifths are 701.96 cents wide, in the exact ratio 3:2, except the wolf fifth, which is only 678.49 cents wide, nearly a quarter of a semitone flatter.

If the notes G♯ and E♭ need to be sounded together, the position of the wolf fifth can be changed. For example, a C-based Pithagorean tuning would produce a stack of fifths running from D♭ to F♯, making F♯-D♭ the wolf interval. However, there will always be one wolf fifth in Pythagorean tuning, making it impossible to play in all keys in tune.

Size of intervals

The table above shows only intervals from D. However, intervals can be formed by starting from each of the above listed 12 notes. Thus, twelve intervals can be defined for each interval type (twelve unisons, twelve semitones, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).

As explained above, one of the twelve fifths (the wolf fifth) has a different size with respect to the other eleven. For a similar reason, each of the other interval types, except for the unisons and the octaves, has two different sizes in Pythagorean tuning. This is the price paid for seeking just intonation. The tables on the right and below show their frequency ratios and their approximate sizes in cents. Interval names are given in their standard shortened form. For instance, the size of the interval from D to A, which is a perfect fifth (P5), can be found in the seventh column of the row labeled D. Strictly just (or pure) intervals are shown in bold font. Wolf intervals are highlighted in red.[5]

The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, the frequencies defined by construction for the twelve notes determine two different semitones (i.e. intervals between adjacent notes):

  1. The minor second (m2), also called diatonic semitone, with size
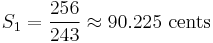
    S_1 = {256 \over 243} \approx 90.225 \ \hbox{cents}
    (e.g. between D and E♭)
  2. The augmented unison (A1), also called chromatic semitone, with size
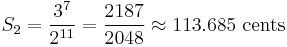
    S_2 = {3^7 \over 2^{11}} = {2187 \over 2048} \approx 113.685 \ \hbox{cents}
    (e.g. between E♭ and E)

Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly

S_E = \sqrt[12]{2} = 100.000 \ \hbox{cents}.

As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.

For a comparison with other tuning systems, see also this table.

By definition, in Pythagorean tuning 11 perfect fifths (P5 in the table) have a size of approximately 701.955 cents (700+ε cents, where ε ≈ 1.955 cents). Since the average size of the 12 fifths must equal exactly 700 cents (as in equal temperament), the other one must have a size of 700−11ε cents, which is about 678.495 cents (the wolf fifth). Notice that, as shown in the table, the latter interval, although enharmonically equivalent to a fifth, is more properly called a diminished sixth (d6). Similarly,

In short, similar differences in width are observed for all interval types, except for unisons and octaves, and they are all multiples of ε, the difference between the Pythagorean fifth and the average fifth.

Notice that, as an obvious consequence, each augmented or diminished interval is exactly 12ε (≈ 23.460) cents narrower or wider than its enharmonic equivalent. For instance, the d6 (or wolf fifth) is 12ε cents narrower than each P5, and each A2 is 12ε cents wider than each m3. This interval of size 12ε is known as a Pythagorean comma, exactly equal to the opposite of a diminished second (≈ −23.460 cents). This implies that ε can be also defined as one twelfth of a Pythagorean comma.

Pythagorean intervals

Main articles: Pythagorean interval and Interval (music)

Four of the above mentioned intervals take a specific name in Pythagorean tuning. In the following table, these specific names are provided, together with alternative names used generically for some other intervals. Notice that the Pythagorean comma does not coincide with the diminished second, as its size (524288:531441) is the reciprocal of the Pythagorean diminished second (531441:524288). Also ditone and semiditone are specific for Pythagorean tuning, while tone and tritone are used generically for all tuning systems. Interestingly, despite its name, a semiditone (3 semitones, or about 300 cents) can hardly be viewed as half of a ditone (4 semitones, or about 400 cents). All the intervals with prefix sesqui- are justly tuned, and their frequency ratio, shown in the table, is a superparticular number (or epimoric ratio). The same is true for the octave.

Number of
semitones		 Generic names Specific names
Quality and number Other naming conventions Pythagorean tuning 5-limit tuning 1/4-comma
meantone
Full Short
0 comma Pythagorean comma
(524288:531441)		 diesis (128:125)
0 diminished second d2 (531441:524288)
1 minor second m2 semitone,
half tone,
half step		 diatonic semitone,
minor semitone		 limma (256:243)
1 augmented unison A1 chromatic semitone,
major semitone		 apotome (2187:2048)
2 diminished third d3 tone, whole tone, whole step
2 major second M2 sesquioctavum (9:8)
3 minor third m3 semiditone (32:27) sesquiquintum (6:5)
4 major third M3 ditone (81:64) sesquiquartum (5:4)
5 perfect fourth P4 diatessaron sesquitertium (4:3)
6 diminished fifth d5 tritone
6 augmented fourth A4
7 perfect fifth P5 diapente sesquialterum (3:2)
12 (perfect) octave P8 diapason duplex (2:1)

History

Because of the wolf interval, this tuning is rarely used nowadays, although it is thought to have been widespread. In music which does not change key very often, or which is not very harmonically adventurous, the wolf interval is unlikely to be a problem, as not all the possible fifths will be heard in such pieces.

Because most fifths in Pythagorean tuning are in the simple ratio of 3:2, they sound very "smooth" and consonant. The thirds, by contrast, most of which are in the relatively complex ratios of 81:64 (for major thirds) and 32:27 (for minor thirds), sound less smooth.[7] For this reason, Pythagorean tuning is particularly well suited to music which treats fifths as consonances, and thirds as dissonances. In western classical music, this usually means music written prior to the 15th century. As thirds came to be treated as consonances, so meantone temperament, and particularly quarter-comma meantone, which tunes thirds to the relatively simple ratio of 5:4, became more popular. However, meantone presented its own harmonic challenges, and its wolf intervals proved to be even worse than those of the Pythagorean tuning (so much so that it often required 19 keys to the octave as opposed to the 12 in Pythagorean tuning), so it is not suitable for all music.

From around the 18th century, as the desire grew for instruments to change key, and therefore to avoid a wolf interval, this led to the widespread use of well temperaments and eventually equal temperament.

Discography

See also

References

Footnotes

  1. ^ a b Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p. 56. Seventh Edition. ISBN 978-0-07-294262-0.
  2. ^ Gunther, Leon (2011). The Physics of Music and Color, p.362. ISBN 9781461405566.
  3. ^ Sethares, William A. (2005). Tuning, Timbre, Spectrum, Scale, p.163. ISBN 1852337974.
  4. ^ Asiatic Society of Japan (1879). Transactions of the Asiatic Society of Japan, Volume 7, p.82. Asiatic Society of Japan.
  5. ^ a b c Wolf intervals are operationally defined herein as intervals composed of 3, 4, 5, 7, 8, or 9 semitones (i.e. major and minor thirds or sixths, perfect fourths or fifths, and their enharmonic equivalents) the size of which deviates by more than one syntonic comma (about 21.5 cents) from the corresponding justly intonated interval. Intervals made up of 1, 2, 6, 10, or 11 semitones (e.g. major and minor seconds or sevenths, tritones, and their enharmonic equivalents) are considered to be dissonant even when they are justly tuned, thus they are not marked as wolf intervals even when they deviate from just intonation by more than one syntonic comma.
  6. ^ Milne, A., Sethares, W.A. and Plamondon, J., "Isomorphic Controllers and Dynamic Tuning: Invariant Fingerings Across a Tuning Continuum", Computer Music Journal, Winter 2007, Vol. 31, No. 4, Pages 15–32.
  7. ^ However, 3/28 is described as "almost exactly a just major third." Sethares (2005), p.60.

Notations

External links

Measurement
Just intonation
Temperaments
6-tone · 12-tone · 15-tone · 17-tone  · 19-tone · 22-tone · 24-tone · 31-tone · 34-tone · 41-tone · 53-tone · 72-tone
Irregular
Traditional non-Western
Non-octave